The earthworker average

published: 29 April 2024 / updated 29 April 2024

Lire cette page en français

 

article: 11 avril 2020 / mis à jour 18 avril 2020

Average calculation

We have all learned to calculate an average. It is enough to make the sum of N numbers and to divide this sum by N. Example:

Many other combinations lead to this average:

Are you starting to understand the problem?

By calculating a gross average, we fail to know whether students are improving, stagnating or are falling. For Mickael, it is obvious that his marks show an impressive improvement, while Charles had a weakness during the quarter. For Henri, it's free fall.

The earthworker average

We're going to see a nifty way to calculate the average in another way, a way which will make it possible in particular to determine if a situation evolves or stagnates.

Take the case of a earthworker who has to fill a piece of land to make it flat in order to build a terrace:

Here, the terrain, from point A is flat to point B, then slopes from point B to point C.

The earthworker must fill the part of land colored green with concrete and aggregates. The height of materials to bring is 10 cm at points A and B, then 20 cm at point C.

If we average the heights in A, B and C, we will have as a result (10+10+20)/3=13.33..

A few months later, our same earthworker has a similar site, but must fill this field:

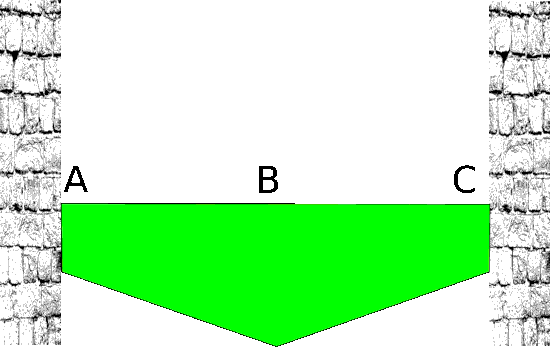
Let’s average the heights A, B and C: (10+20+10)/3=13.33..

However, there is not at all - but then really not at all - the same volume material to pour.

To calculate the volume of material to bring, we can do a geometry calculation. For our part, we will approach the problem in another way.

Averages of averages

The midpoint between A and B has a height which will be the value average of the heights measured in A and B. It is the same for the midpoint located between B and C. Let's find the calculation of these average heights here:

A B C
10  10  20
 10  15 

 

We obtain two averages which seem to correspond to the heights of land to be filled:

The average of these means M1 and M2 will be (M1 + M2) / 2 = 12.5

Let’s repeat the calculation of these averages, applied to the second earthwork case:

A B C
10  20  10
 15  15 

 

Calculation of the two means:

The average of these means M1 and M2 will be (M1 + M2) / 2 = 15

Just by changing the order of the initial data, we don't get the same average average! The results seem to correspond to the average height of the material to bring to develop the land of our earthworker ...

General application

Let's apply this averaging calculation to the grades of our students:

Mickael:

A B C
10  10  20
 10  15 
  12.5   

 

Charles:

A B C
16  10  14
 13  12 
  12.5   

 

Henri:

A B C
18  17  5
 17.5  11 
  14.25   

 

For reasons of convenience, let us abbreviate by Mt this average of means.

Let's analyze these results:

Formalisation

To calculate an average Mt of 3 values A, B and C, here is the general formula:

Mt = ( ( ( A + B ) / 2 ) + ( ( B + C ) / 2 ) ) / 2
   = ( ( A + B + B + C ) / 2 ) / 2
   = ( A + 2B + C ) / 4

So we have a divider, here 4.

It is therefore not necessary to do the intermediate averages. Just do the are intermediate:

Henri:

A B C
18  17  5
 35  22 
  57   

 

Here, the final result 57/4 = 14.25 .

The divider 4 is equal to 2 exp 2. 2 is equal to the number of elements, here 3, value to which we subtract 1.

Does it work with 4 values? Let's do the test:

Charles:

A B C D
16  10  14  11
 13  12  12.5 
  12.5  12.25   
   12.375    

 

The Mt value is here 12.375.

The same table, but with the sums:

A B C D
16  10  14  11
 26  24  25 
  50  49   
   99    

 

With 4 elements, our divider will be 2 EXP 4-1 = 8

99/8 = 12.375

In passing, we will notice that 99 is the sum of the values 50 and 49, these values indicating a slight drop.

The value 50 results from the application of this formula:

MtX = ( A + 2B + C ) / 4

The value 49 results from the application of this formula:

MtY = ( B + 2C + D ) / 4

The sum Mt, of value 99, therefore results from this formula:

Mt = ( ( ( A + 2B + C ) / 4 ) + ( ( B + 2C + D ) / 4 ) ) / 2
   = ( ( A + 3B + 3C + D ) / 4 ) / 2
   = ( A + 3B + 3C + D ) / 8

We find these multiplicative factors, for (A + 3 B + 3C + D) / 8 , here 1 3 3 1, in Pascal's triangle:

In Pascal's triangle, the sum of the terms on the row of rank n (first line = rank 0) is equal to 2 EXP n. It is this sum of terms which we use as a divisor to calculate the Mt value. Example, for the result 99, Mt = 99 / ( 1 + 3 + 3 +1 ), i.e. 99/8.

Application in FORTH language

Here, you will find the development, in FORTH language, of the calculation of the average of the earthworker. There are two versions, one for gForth which processes data natively in 32 bits, the other for FlashForth which uses a 16-bit stack. The differences between these two developments lead to the same results.

For gForth

Specific gForth

The complete source code is available here.

We define an array of n values, here 5, stored in the array initValues. gForth stores these values in 32-bit format:

5 constant nbValues         \ number of initials values 
\ compile initials values 
create initValues  
    16 ,    10 ,    14 ,    11 ,   18 , 
\ display values in array 
: .values ( adr n ---) 
    0 do 
        dup i cell * +      \ calculate address of a value 
        @ cr .              \ fetch and display value 
    loop ;

Example of using .values. This word displays n values of an array:

initValues nbValues .values     \ display:
16
10
14
11
18  ok

We then define two other tables, calcBuffer which will be used to store the intermediate values, finalValues which stores the final result:

create calcBuffer 
    nbValues cell * allot 
create finalValues  
    nbValues cell * allot

The word finalToBuffer copies n values from finalValues to calcBuffer:

: finalToBuffer ( n ---) 
    cell * >r 
    finalValues calcBuffer r> cmove 
  ;

The variable calcDepth is used to store the level of calculations to be processed. Every recalculation of means, the content of this variable is decremented.

The word calcAverage is responsible for calculating the intermediate averages. If the content of the variable calcDepth is not equal to one, the function is re-executed by recursion:

\ calculate eartworker average 
variable calcDepth 
: calcAverage ( ---) 
    -1 calcDepth +! 
    calcDepth @  0 do 
        calcBuffer  i    cell * + @     \ get first value in buffer 
        calcBuffer  i 1+ cell * + @ +   \ get second value in buffer and add 
        finalValues i    cell * + !     \ store result 
    loop 
    calcDepth @ 1 >  
    if 
        calcDepth @ finalToBuffer 
        recurse 
    then 
  ;

The word calculate launches a final sum calculation session from which we will obtain the average Mt.

: calculate ( ---) 
    \ move initial values in buffer 
    initValues calcBuffer nbValues cell * cmove 
    \ set initial value of calcDepth 
    nbValues calcDepth ! 
    \ start average calculation 
    calcAverage 
  ;

For FlashFORTH

The FORTH version for Flashforth uses 16-bit data. It was therefore necessary to make certain adjustments to be able to process data of the same size as on gForth, i.e. 32-bit data:

-average 
marker -average 
\ convert integer in double and compile 
: 2, ( n --- ) 
    s>d swap , , ; 
 
\ calculate a 32 bits offset, example: 
: 2offset ( n --- n' ) 
    cell 2* * ; 
 
\ calculate real address for 32 bits content of array, example: 
: 2addr.offset ( addr offset --- addr' ) 
    2offset + ;

We find our initial data table in initValues:

5 constant nbValues         \ number of initials values 
flash 
\ compile initials values 
create initValues  
    16 2,    10 2,    14 2,    11 2,   18 2,

The words i and i+ are defined to compensate for the absence the do..loop loop in FlashForth:

\ calculate index starting from 0 
ram 
variable startIndex 
: i ( --- i )   \ create word i that not defined in FlashForth 
    startIndex @ 
  ; 
: i+  ( ---)    \ increment index 
    1 startIndex +! 
  ;

Here we find the word .values where the DO..LOOP loop has been replaced by a for..next loop:

\ display values in array 
: .values ( adr n ---) 
    0 startIndex ! 
    for 
        dup                 \ duplicate initial address 
        i                   \ get loop index 
        2addr.offset        \ calculate offset in 2array     
        2@ d.               \ fetch and display value 
        i+ 
    next  
    drop  
  ; 
 
ram 
\ calculate eartworker average 
create calcBuffer 
    nbValues 2offset allot 
create finalValues  
    nbValues 2offset allot 
 
eeprom 
: finalToBuffer ( n ---) 
    2offset >r 
    finalValues calcBuffer r> cmove 
  ; 
 
ram 
variable calcDepth 
eeprom

Then in the word calcAverage, the recursion gives way to a loop begin..while..repeat, because under FlashForth, the depth of stacks of data and return are very limited:

: calcAverage ( ---) 
    begin 
        -1 calcDepth +! 
        0 startIndex ! 
        calcDepth @  for 
            calcBuffer  i    2addr.offset  2@ 
            calcBuffer  i 1+ 2addr.offset  2@  d+ 
            finalValues i    2addr.offset 2! 
            i+ 
        next 
        calcDepth @ 1 > 
    while 
        calcDepth @ finalToBuffer 
    repeat 
  ; 
 
: calculate ( ---) 
    initValues calcBuffer nbValues 2offset cmove 
    nbValues calcDepth ! 
    calcAverage 
  ;

Result of the execution of calculate:

initValues nbValues .values cr 16 10 14 11 18
 ok<#,ram>
calcBuffer 2 .values cr 99 103
 ok<#,ram>
finalValues 2@ d. cr 202
 ok<#,ram>

Analysis of the calculation result

Whether for gForth or for FlashForth, to test the calculation the average of the earthworker for the values stored in the initValues table, just execute these words like this:

calculate
initValues nbValues .values cr
calcBuffer 2 .values cr
finalValues @ . cr

Display of the execution under gForth:

calculate  ok
  ok
initValues nbValues .values cr
16
10
14
11
18
 ok
calcBuffer 2 .values cr
99
103
 ok
finalValues @ . cr 202
 ok

The word calculate starts the earthworker's average calculation sequence.

The sequence initValues ​​nbValues ​​.values ​​cr displays the initial values contained in the initValues table: 16 10 14 11 1

The sequence calcBuffer 2 .values ​​cr displays the last pair of values ​​the sum of which will be the value from which the average Mt will be calculated, here 99 103:

And finally, the sequence finalValues ​​@. cr displays the final sum from which we can calculate the average Mt, here 202

The average MT will be calculated according to the formula 202 / (2 EXP nbValues-1), that is 202/16.

What can it be used for?

It's a great question and thank you for asking it.

We started this article by dealing with school grades for students; The average Mt actually has no interest in dealing with student averages.

On the other hand, calculating the average Mt can be very useful in many areas.

We are going to take a very simple example, the case of a central heating boiler which must be triggered if the temperature of a probe drops below 19 ° C. The concern is that this probe tends to trigger in an intenpestive way, which triggers many starting and stopping of the central heating boiler.

The idea is therefore to treat by average Mt only the last six temperature measurements, here measurements performed every 10 minutes:

In the first case, although the measurement is temporarily at 18°C (fourth value), the mean Mt being higher at 19, the boiler does not turn on.

The second case corresponds to the last three temperature measurements of the first line, at which are added the 17 18 18 smesures. The average Mt drops below 19 and the boiler will ignite.

The average Mt will therefore apply to a limited sample of values. For example, to follow the evolution of sales of products over a week, we will take the last 7 sales values. If every day we collect the 7-day rolling figures, it will be possible to obtain a downward, upward trend or no trend evolution of these sales.

To conclude, we have processed, for gForth and FlashForth whole data in format 32 bit. The Mt calculation also works with negative values. If your version of the Forth language has the functions floating point calculation, you are free to adapt the Forth code.