Example of the use of infix notation

published: 28 June 2020 / updated 28 June 2020

Preamble

The infixed notation is an opportunity to show an interesting aspect operations by mixing algebraic operators and logical operators.

To do this, we start from a challenge consisting in programming operations allowing to restore this image under gForth:

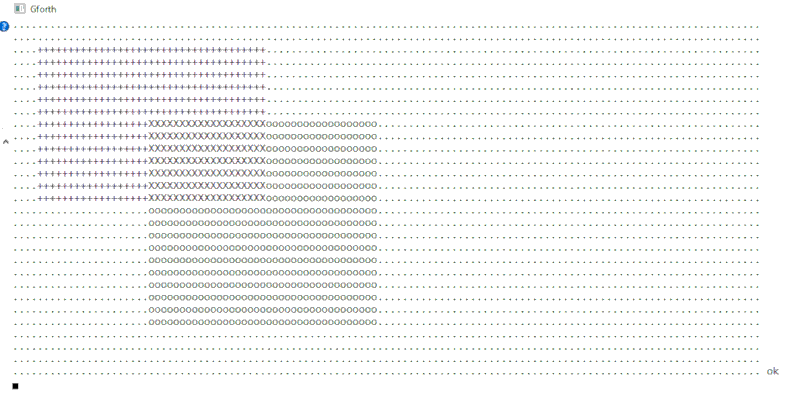
In a frame of 120 columns on 30 lines, we display two rectangles:

the first rectangle is filled with "+" characters, the second with "o" characters
at the intersection of these two rectangles, we fill with "X" characters
outside these two rectangles, we fill with the character "."

How to manage the selection of the character to display only using arithmetic and logical formulas?

Viewing and managing the content of rectangles

In any space, here a screen in text mode, we must display two rectangles:

We are in text mode. The cursor cannot be positioned on our space display only by displaying a character in a line, then switching to the next line.

Depending on its position, the cursor must display one of these four characters: . + X and o. In the figure above, the cursor position is pointed by two variables DX and DY.

Compile the contents of the infix.txt file beforehand.

The full code is available here: infix.txt

It must be compiled with gForth.

The program must send 120 characters per line, this on 30 lines.

0 value DX      \ current X coordinate
0 value DY      \ current Y coordinate
 
: dx+  ( ---)   \ increment DX 1 position
    DX 1+ to DX ;
 
: dy+  ( ---)   \ increment DY 1 position
    DY 1+ to DY ;

The DX DY variables store the cursor position. The content of these variables is handled as follows:

for each character sent, we increment DX with the word dx+
at the end of each line, we reset the contents of DX and we increment the content of DY with the word dy+

Logical processing of the cursor position

The dimensions of a rectangle are determined by four variables SX EX SY EY (SX pour Start X...):

0 value SX    \ x Start rect 1
0 value EX    \ x End   rect 1
0 value SY    \ y Start rect 1 
0 value EY    \ y Etart rect 1

It is therefore necessary to determine whether the cursor position is located in a rectangle. Here is the logic formula delivering a Boolean flag depending on the position of the cursor:

( NOT ( DX < SX ) ) AND ( NOT ( DX > EX ) ) AND ( NOT ( DY < SY ) ) AND ( NOT ( DY > EY ) )

Voyons en détail le premier membre de cette formule logique:

( NOT ( DX < SX ) )

To find out if DX is inside a rectangle, we have two possibilities:

by formulating by inclusion: DX >= SX. But, the operator >= is not defined in the file infix.txt
by formulating by exclusion: NOT (DX < SX). This solution is suitable because > is defined in the infix.txt file

Here is the coding of this formula in infix notation:

: inRect? ( --- fl)
    $[      ( NOT ( DX < SX  ) ) AND 
            ( NOT ( DX > EX  ) ) AND 
            ( NOT ( DY < SY  ) ) AND 
            ( NOT ( DY > EY  ) )
    ]$  ;

The word inRect? will issue a Boolean flag if DX DY is in the rectangle whose dimension is indicated by the content of the variables SX EX SY EY.

Once compiled, we can see what has become of our infix formula by typing see inRetc? from the FORTH interpreter, which displays this:

see inRect?
: inRect?
  DX SX < invert DX EX > invert and DY SY < invert and DY EY > invert and ; ok

The compilation of a formula in infixed notation restores a perfectly optimized FORTH code!

Treatment of different logical cases

We will now approach the different logical situations allowing to select the character to display. To do this, let's name leftRect the left rectangle, then rightRect the right rectangle. We can already define two words restoring a Boolean flag if the cursor is in one of these two rectangles:

: inLeftRect? ( --- fl)
    4  to SX    \ x Start rect left
    40 to EX    \ x End   rect left
    4  to SY    \ y Start rect left 
    16 to EY    \ y Etart rect left 
    inRect?  ;
 
: inRightRect? ( --- fl)
    22 to SX    \ x Start rect right
    58 to EX    \ x End   rect right
    10 to SY    \ y Start rect right 
    26 to EY    \ y Etart rect right 
    inRect?  ;

With these parameters, our two rectangles share a common area. We will see later how to treat this case.

The display cursor must therefore manage four situations:

if the cursor is not in leftRect and rightRect, we display the character "." /li>
if the cursor is in leftRect but is not in rightRect, we display the character "+"
if the cursor is not in leftRect but is in rightRect, we display the character "o"
if the cursor is in leftRect and in rightRect, we display the character "X"

Take the first case: the cursor is not in leftRect and rightRect.

The logical formula part will be of the form:
( NOT inLeftRect? ) AND ( NOT inRightRect? )

This part of code will restore a Boolean flag whose numeric value will be 0 ou -1.

If we then execute the word abs after this Boolean flag, we will have two results:0 or 1
( NOT inLeftRect? ) AND ( NOT inRightRect? ) abs

The ASCII code for the character "." is 46. We multiply this ASCII code by the result of our formula:
46 * ( ( ( NOT inLeftRect? ) AND ( NOT inRightRect? ) ) abs )

Let's put this formula in a new word:

: dispChar ( ---)
    $[    \ 46  is char .
            46  * ( ( ( NOT inLeftRect? ) AND ( NOT inRightRect? ) ) abs
    ]$
    emit
  ;

Take the second case: the cursor is in leftRect but is not in rightRect.

The logical formula part will be of the form:
( inLeftRect? ) AND ( NOT inRightRect? )

In this second case, the ASCII code for the "+" character is 43. We multiply this ASCII code by the result of our formula:
43 * ( ( ( inLeftRect? ) AND ( NOT inRightRect? ) ) abs )

We now have two formulas, which return either 0 or the ASCII code of the character to display. Our word dispChar becomes:

: dispChar ( ---)
    $[    \ 46  is char .
          ( 46  * ( ( ( NOT inLeftRect? ) AND ( NOT inRightRect? ) ) abs ) )
          \ 43  is char +
        + ( 43  * ( ( ( inLeftRect? ) AND ( NOT inRightRect? ) ) abs ) )
    ]$
    emit
  ;

We already have two situations: 46 + 0 ou 0 + 43...

Two cases remain to be dealt with. Here is the full definition of the word dispChar taking into account all cases:

: dispChar ( ---)
    $[    \ 46  is char .
          ( 46  * ( ( ( NOT inLeftRect? ) AND ( NOT inRightRect? ) ) abs ) )
          \ 43  is char +
        + ( 43  * ( ( ( inLeftRect? ) AND ( NOT inRightRect? ) ) abs ) )
          \ 88  is char X
        + ( 88  * ( inLeftRect? AND inRightRect? abs ) )
          \ 111 is char o
        + ( 111 * ( ( ( inRightRect? ) and ( NOT inLeftRect? ) ) abs ) )
    ]$
    emit
  ;

In this definition, we restore a single ASCII character whose code is adapted to the cursor position, all without any if..then or equivalent test.

Here is what decompilation of the word dispChar gives:

see dispChar
: dispChar
  46 inLeftRect? invert inRightRect? invert and abs * 43 inLeftRect?
  inRightRect? invert and abs * + 88 inLeftRect? inRightRect? abs and * + 111
  inRightRect? inLeftRect? invert and abs * + emit ; ok

Boucles d'affichage

In the word graphLoop we manage two nested loops. In the loop inside, we treat the display of the character with the word dispChar then we increment the value of DX with the word dx+.

In the outer loop, we increment the value of DY with the word dy+ then we reset the content of DX:

: graphLoop ( ---)
    30 for
        cr
        120 for
            dispChar
            dx+
        next
        dy+
        0 to DX
    next ;

Conclusion

The content of this article is a pure exercise in style.

However, it addresses an interesting concept, that of programming without conditional connection.

Here is a video showing how Von NEUMANN's elephant is made:

Watch this video at 8'50 ", you will find there a very nice formula for drawing an elephant:

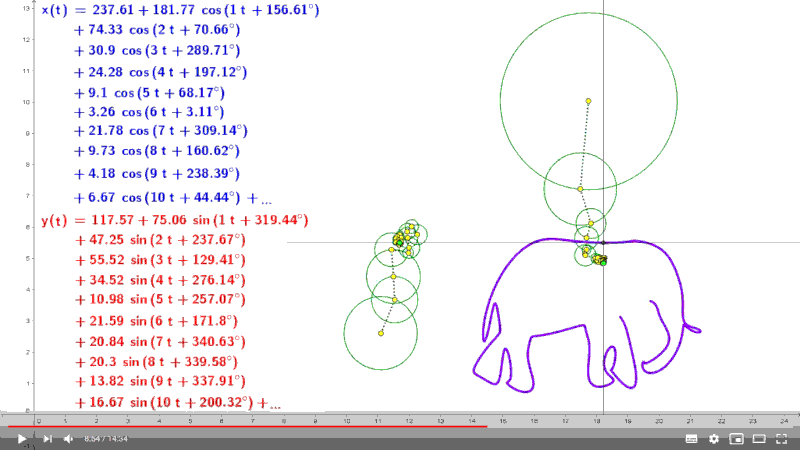
Here is a very nice challenge for FORTH by modifying the infix notation for apply it to floating numbers.